Sipu Ruan ¹, Karen L. Poblete ², Hongtao Wu ³, Qianli Ma ⁴ and Gregory Chirikjian ¹

¹ Department of Mechanical Engineering, National University of Singapore, Singapore

² Epic Systems, Verona, WI, USA

³ Laboratory for Computational Sensing and Robotics, Johns Hopkins University, Baltimore, MD, USA

⁴ Motional Inc., Pittsburgh, PA, USA

Published in IEEE Transactions on Robotics (T-RO)

Introduction

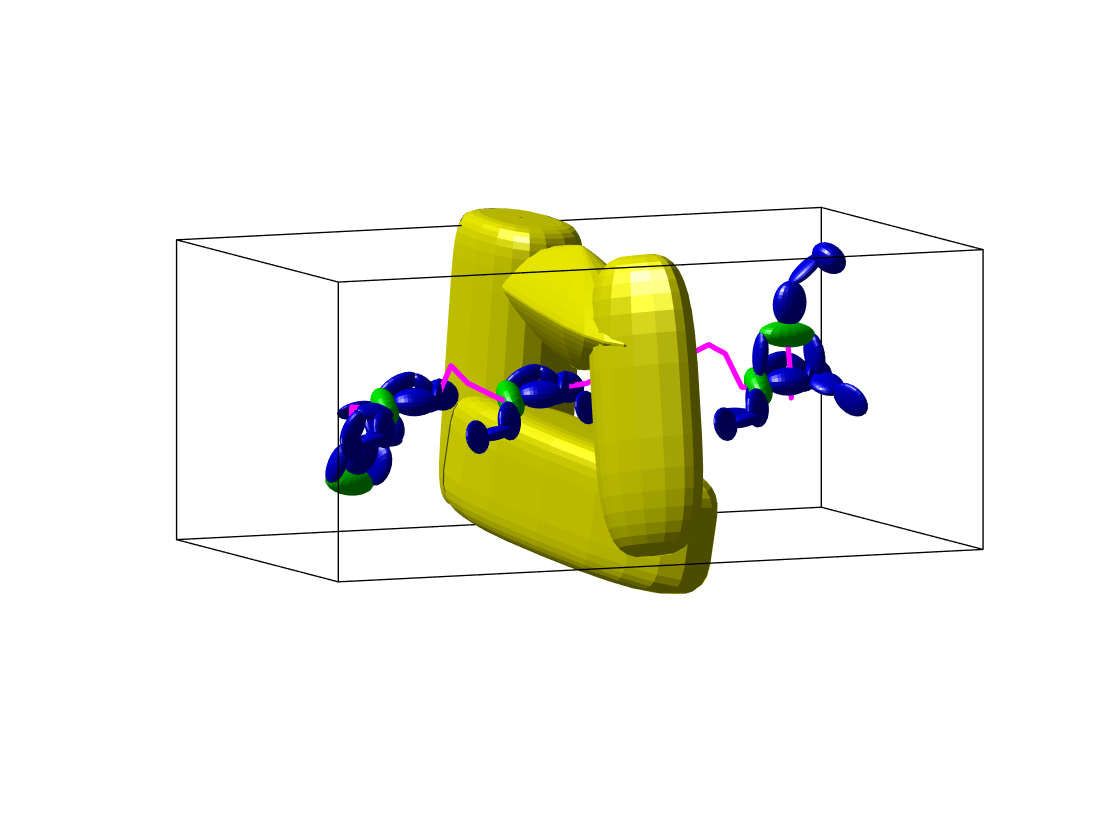
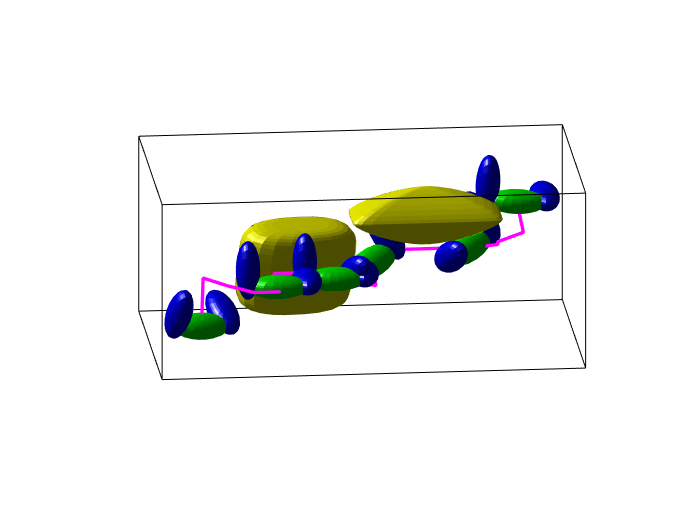
Path planning has long been one of the major research areas in robotics, with PRM and RRT being two of the most effective classes of planners. Though generally very efficient, these sampling-based planners can become computationally expensive in the important case of “narrow passages”. This paper develops a path planning paradigm specifically formulated for narrow passage problems. The core is based on planning for rigid-body robots encapsulated by unions of ellipsoids. Each environmental feature is represented geometrically using a strictly convex body with a C¹ boundary (e.g., superquadric). The main benefit of doing this is that configuration-space obstacles can be parameterized explicitly in closed form, thereby allowing prior knowledge to be used to avoid sampling infeasible configurations. Then, by characterizing a tight volume bound for multiple ellipsoids, robot transitions involving rotations are guaranteed to be collision-free without needing to perform traditional collision detection. Furthermore, by combining with a stochastic sampling strategy, the proposed planning framework can be extended to solving higher dimensional problems in which the robot has a moving base and articulated appendages. Benchmark results show that the proposed framework often outperforms the sampling-based planners in terms of computational time and success rate in finding a path through narrow corridors for both single-body robots and those with higher dimensional configuration spaces. Physical experiments using the proposed framework are further demonstrated on a humanoid robot that walks in several cluttered environments with narrow passages.

Links

• Paper: T-RO, Arxiv
• Code:
  • Source code: https://www.github.com/ChirikjianLab/hrm/
  • API documentation: v1.0.0 (latest)

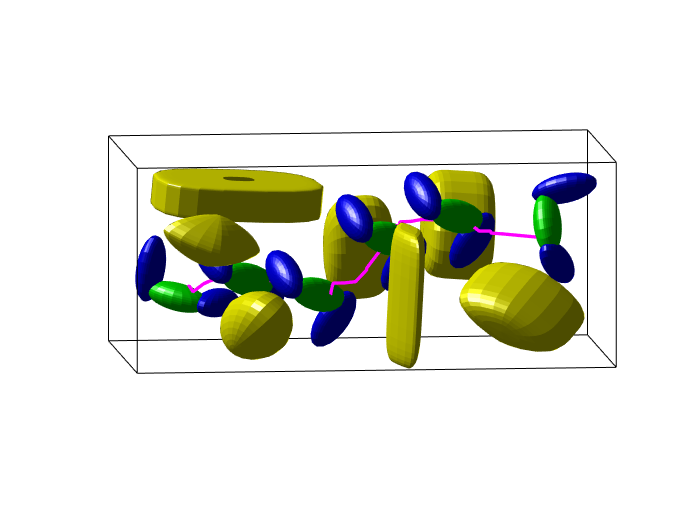
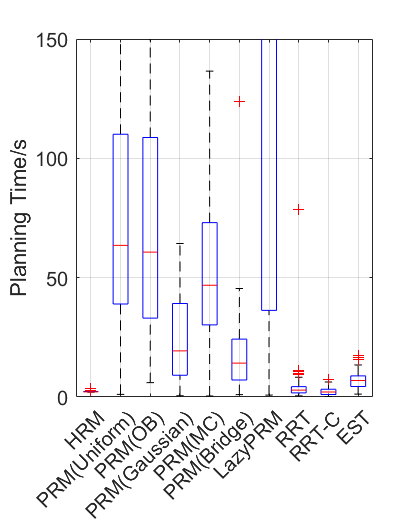
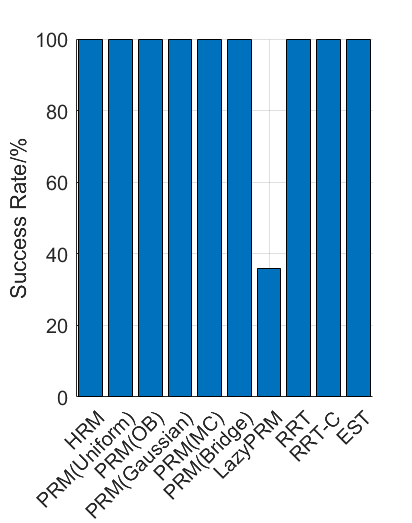
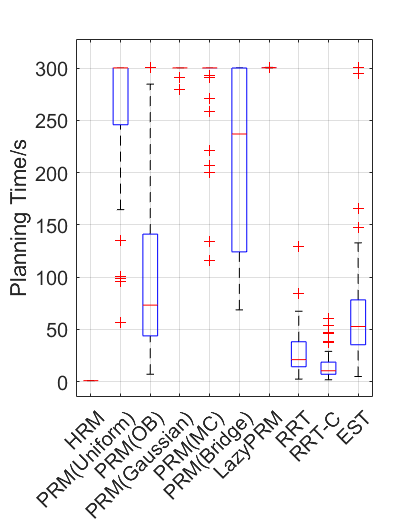
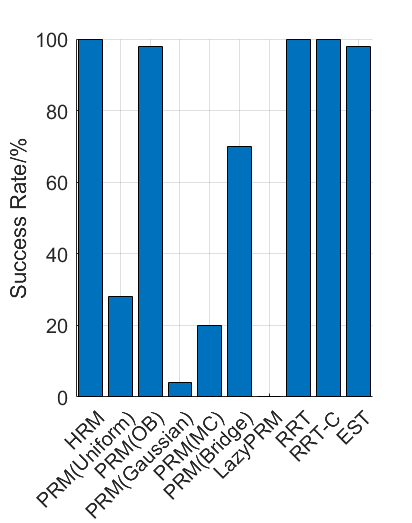
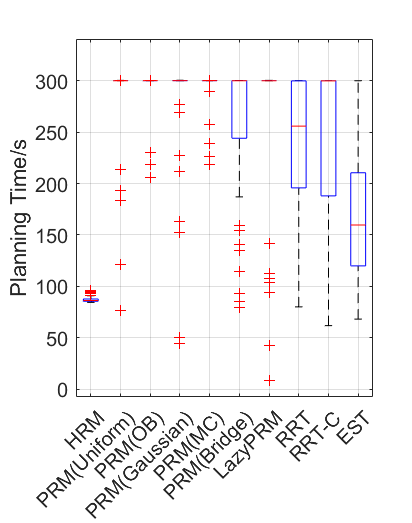
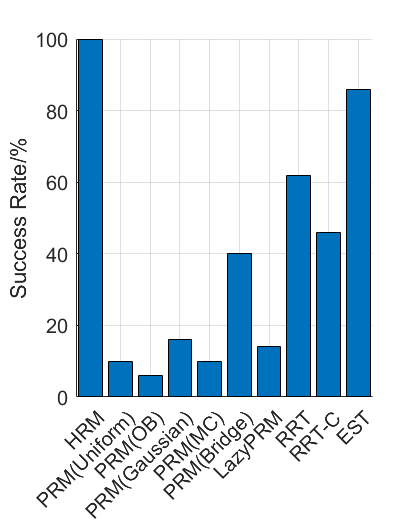
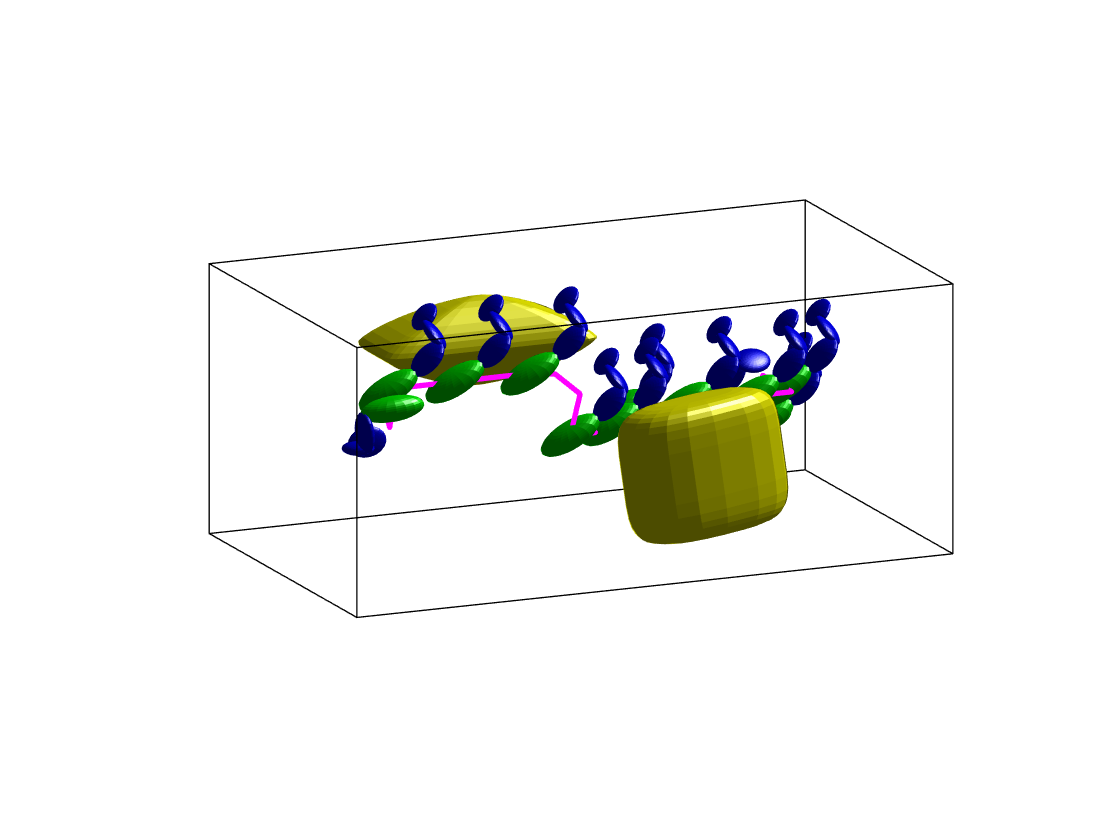
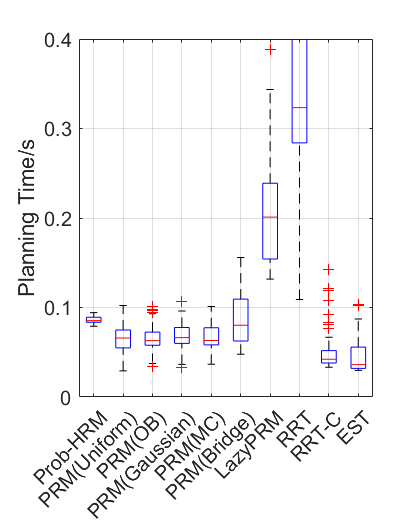
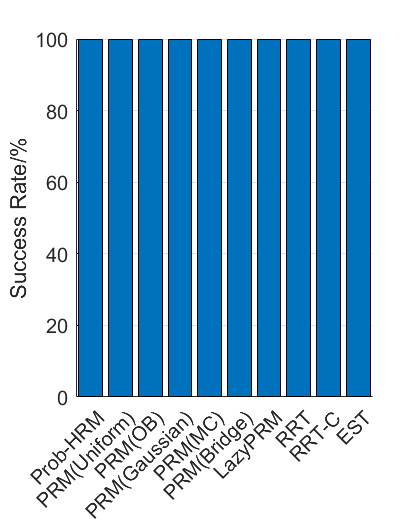
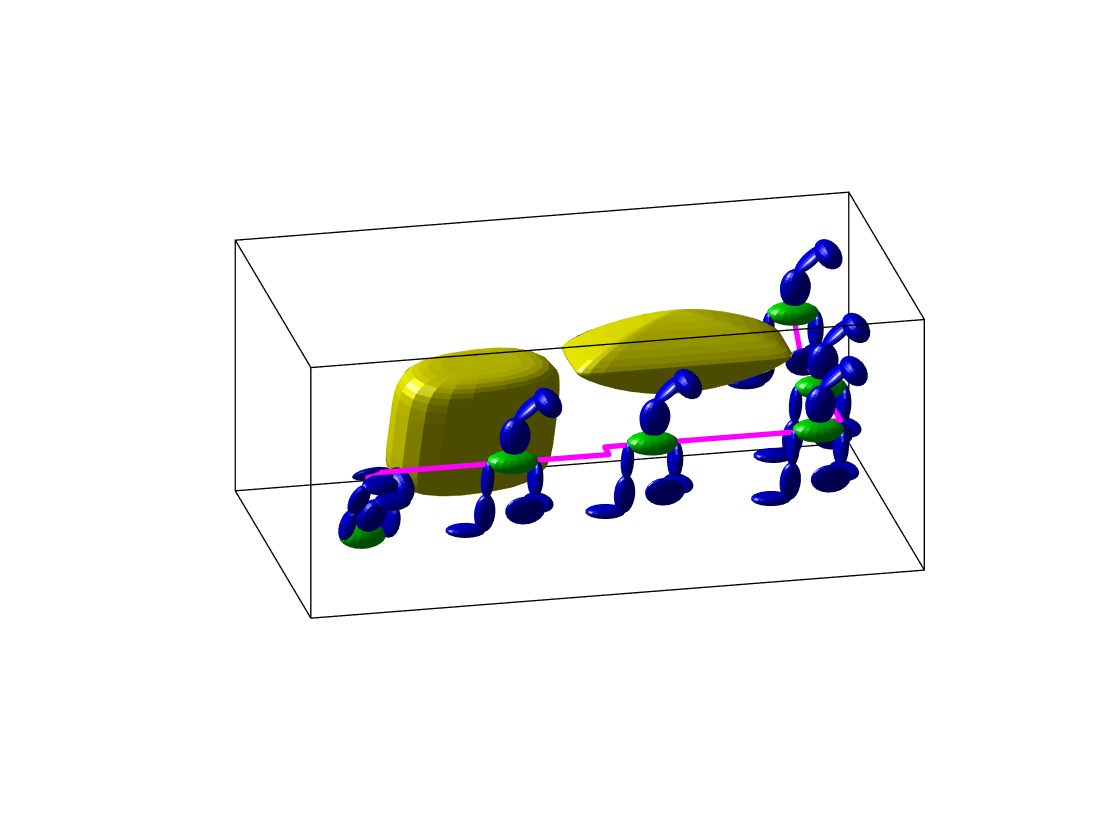
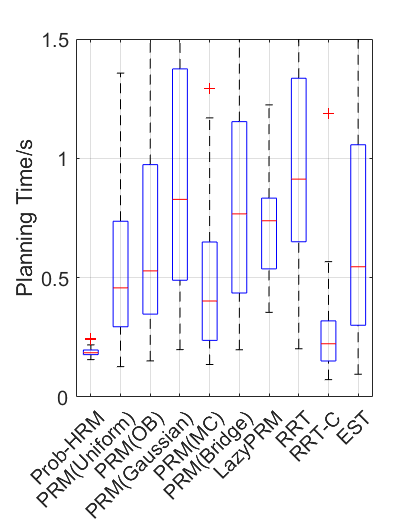
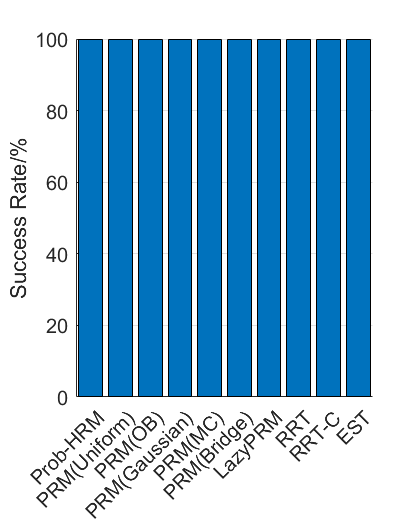
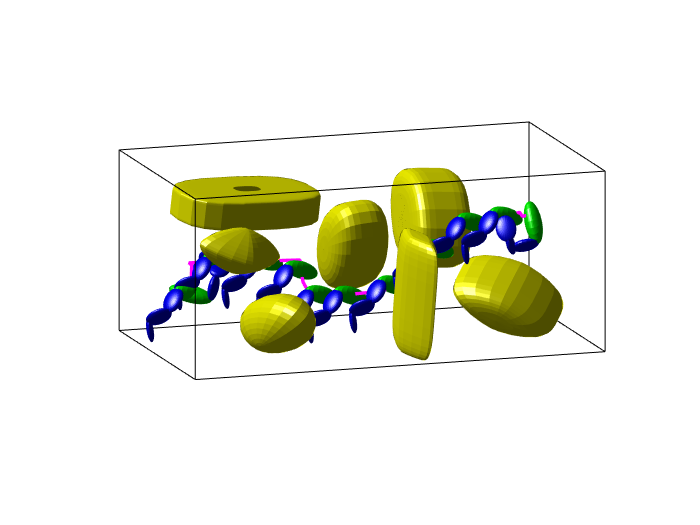
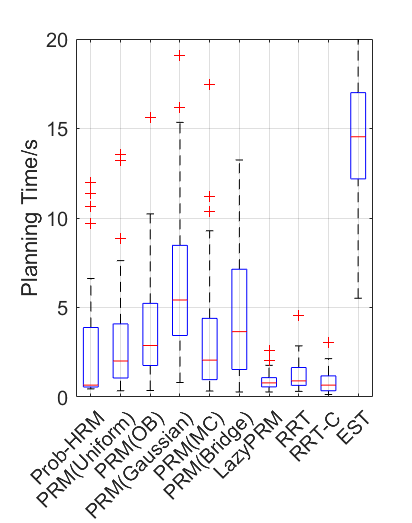
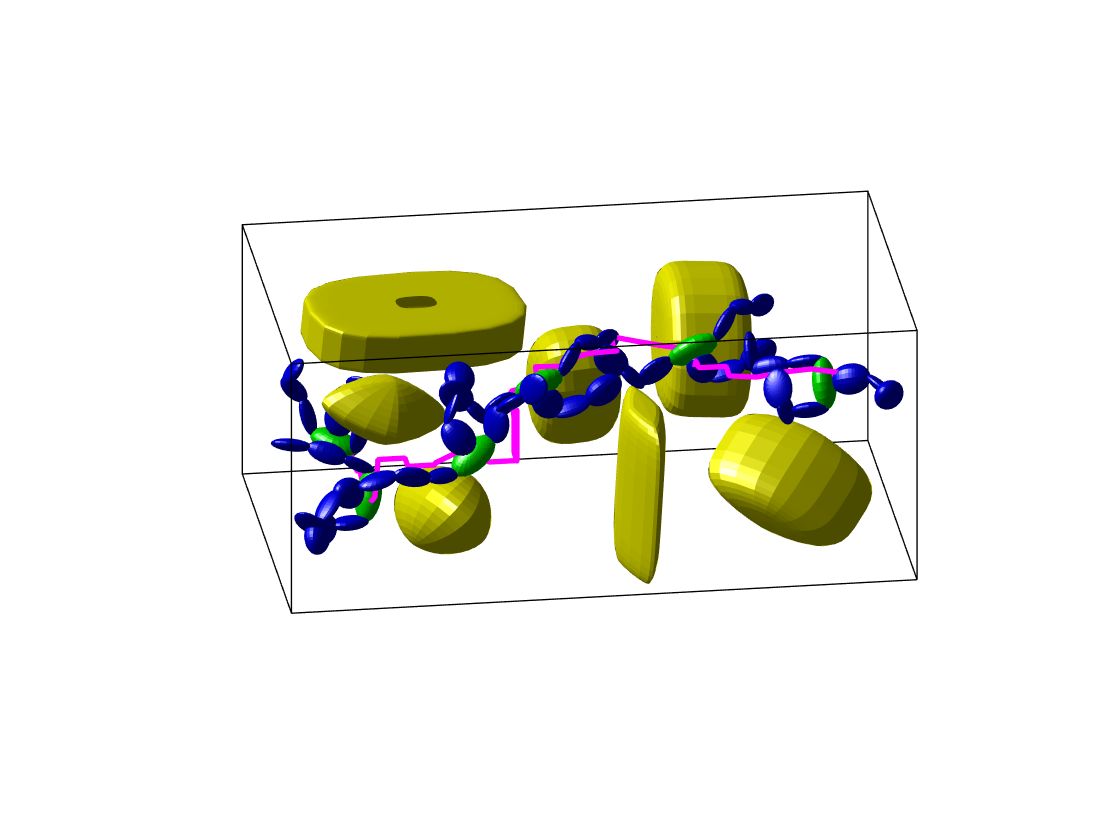
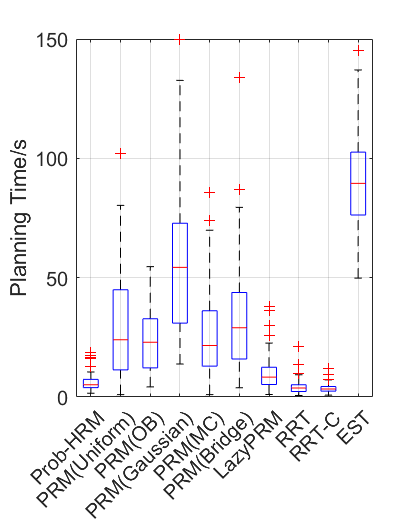
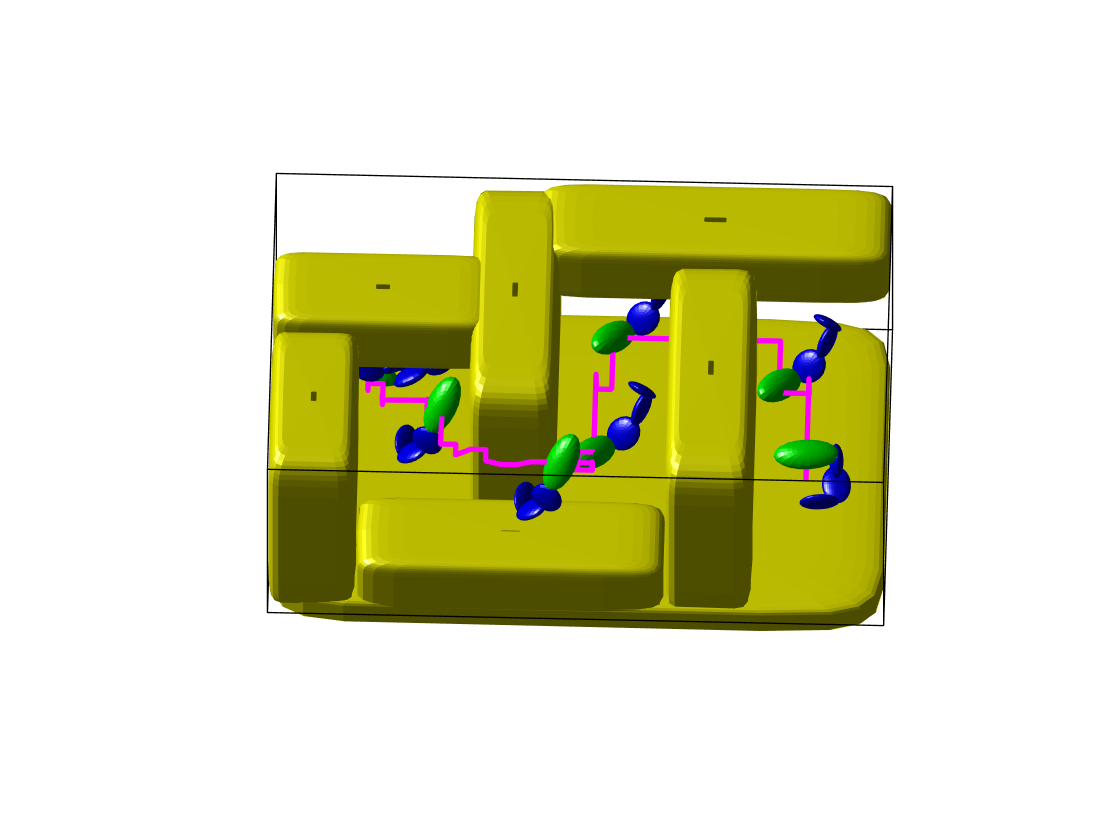
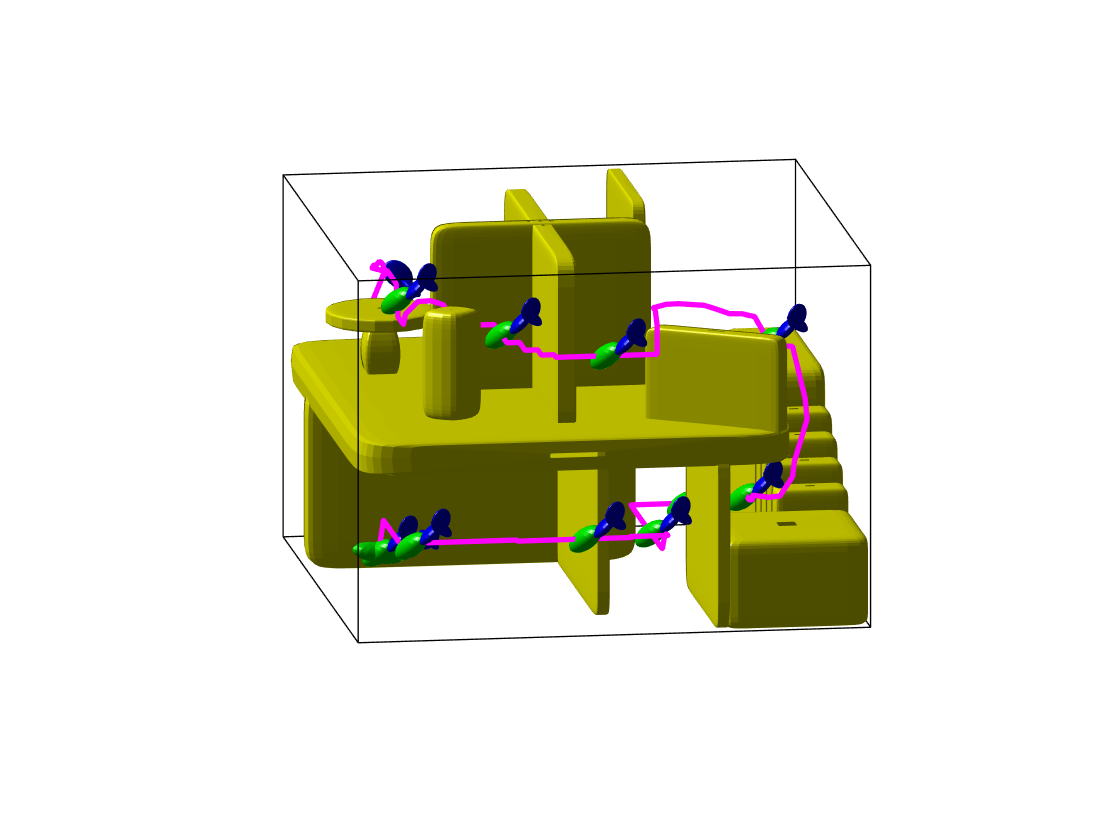
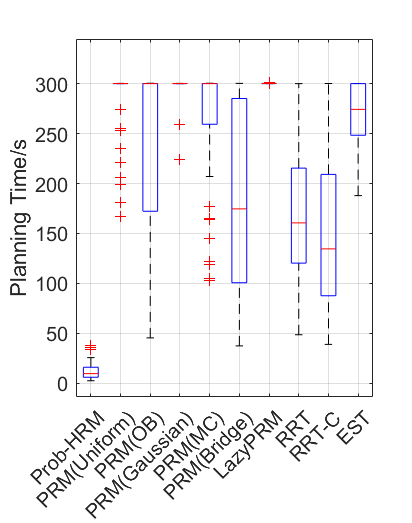
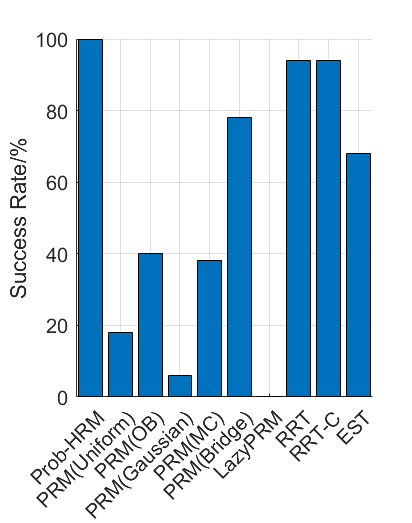
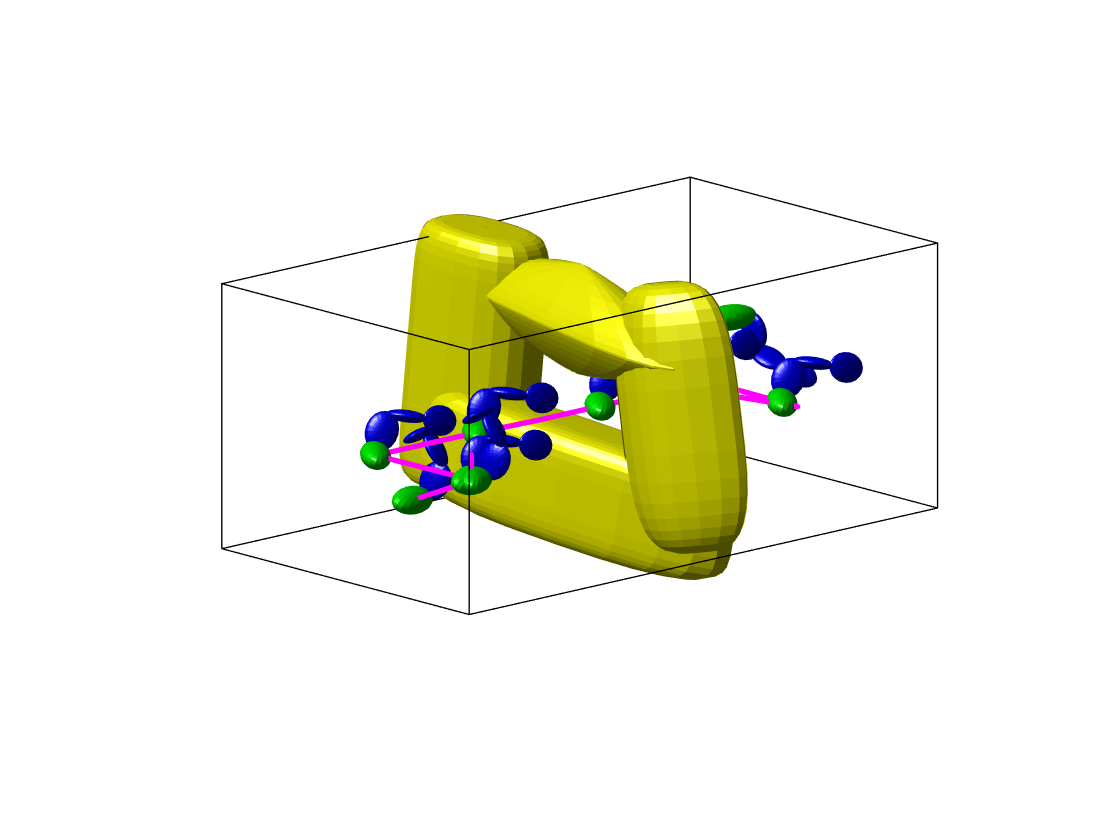
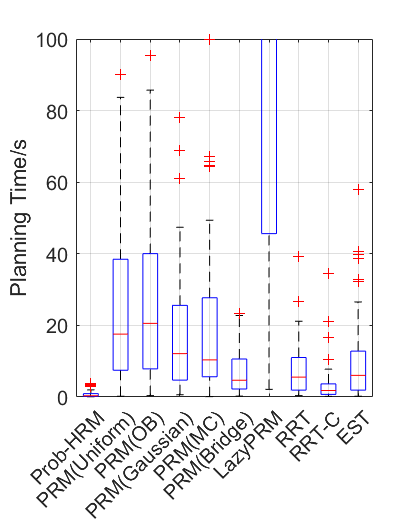
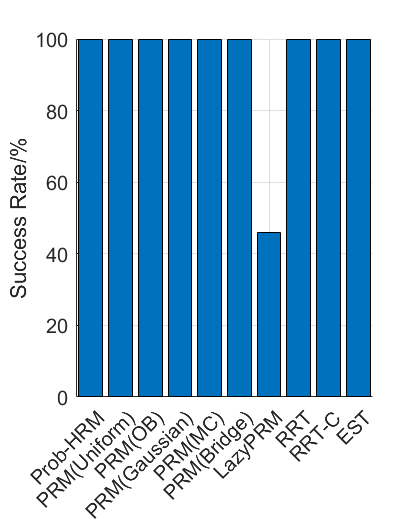
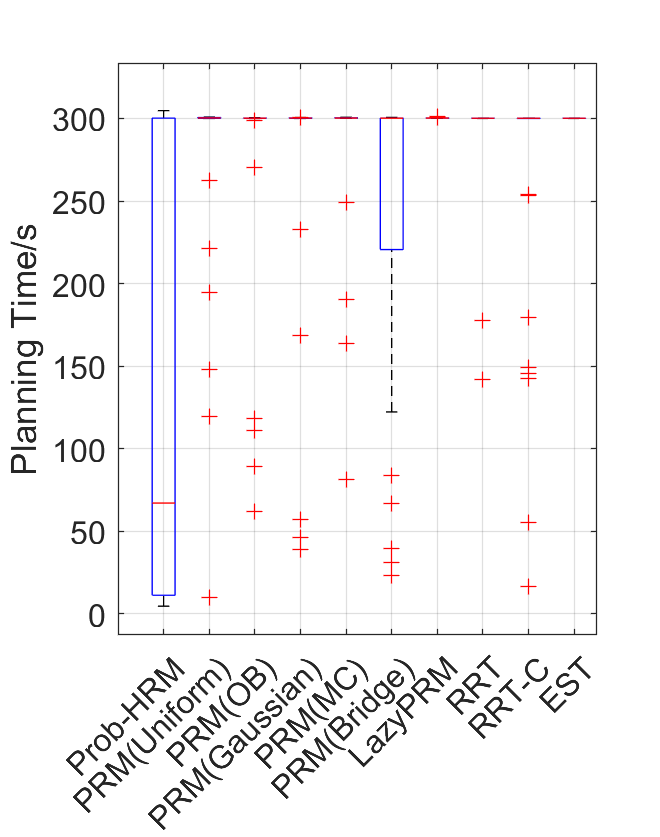
Benchmark experiments

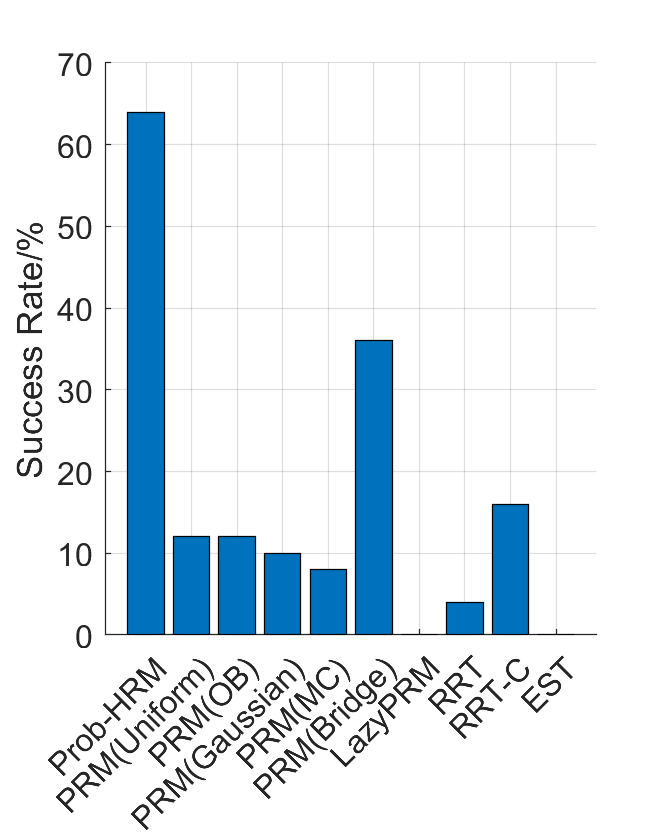
Baselines: PRM (with various samplers), LazyPRM, RRT, RRT-connect, EST.

Choose a planning scene: Sparse environment; Rabbit-like robot Cluttered environment; Rabbit-like robot Maze environment; Rabbit-like robot Home environment; Chair object Sparse environment; Snake-like robot Sparse environment; Tree-like robot Cluttered environment; Rabbit-like robot Cluttered environment; Tree-like robot Maze environment; Snake-like robot Home environment; Snake-like robot Narrow environment; Snake-like robot Narrow environment; Tree-like robot

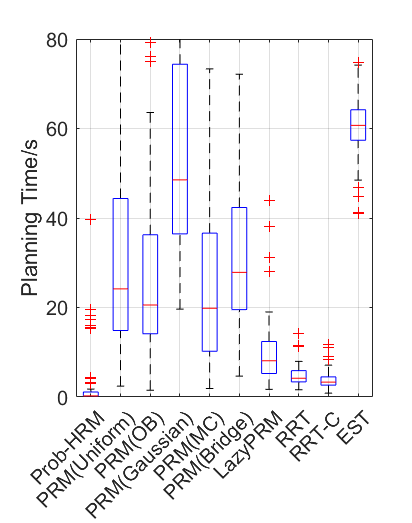
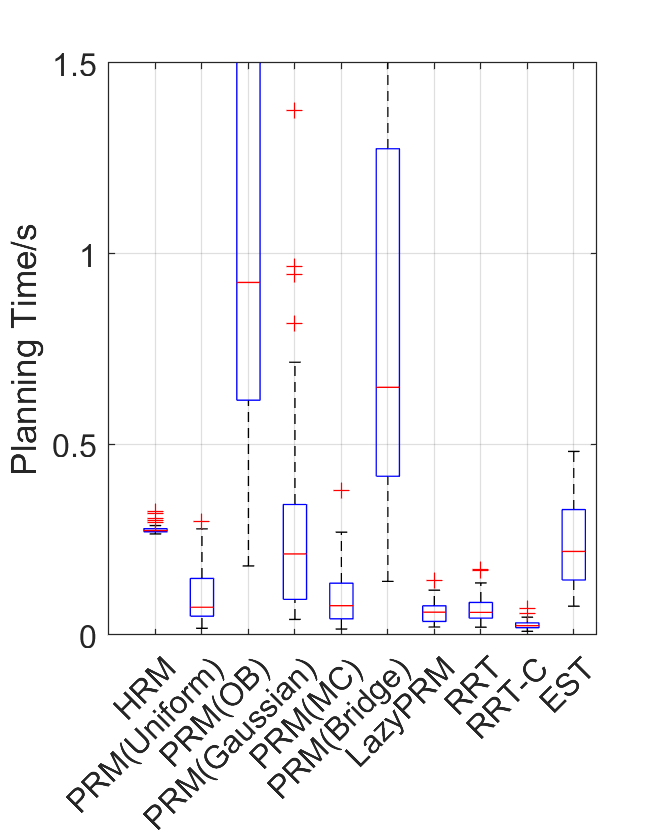
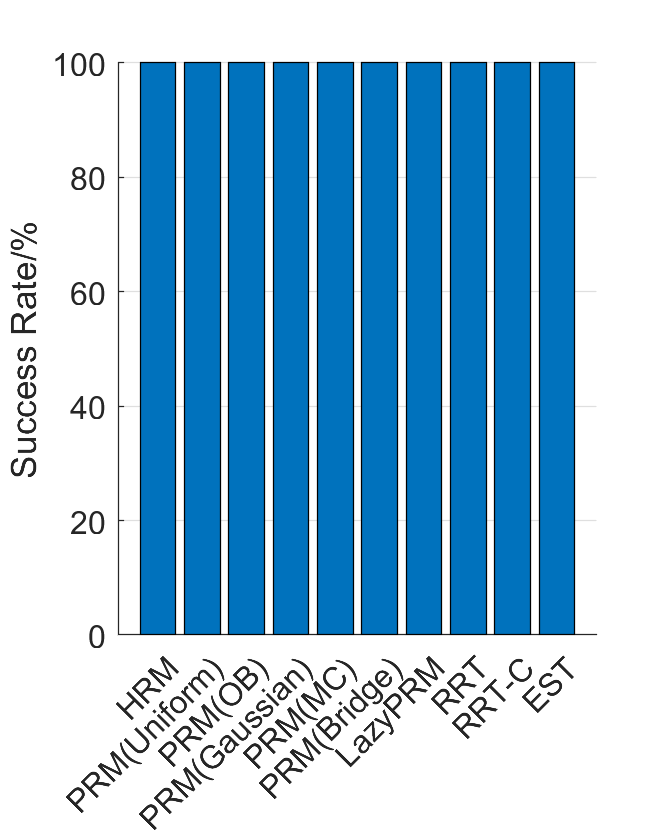
Benchmark results

Planning scene	Solving time	Success rate

Parameters for HRM (rigid)/Prob-HRM (articulated) planner

Initial input number		Number after planning (averaged over 50 trials)
C-slices	Sweep lines (grid size)	C-slices	Sweep lines
60	10 (5 x 2)	60	10
60	55 (11 x 5)	60	55
60	55 (11 x 5)	60	55
60	400 (20 x 20)	60	400
--	18 (6 x 3)	2	18
--	18 (6 x 3)	2	18
--	72 (12 x 6)	9	72
--	72 (12 x 6)	9	72
--	72 (12 x 6)	16	102
--	400 (20 x 20)	11	400
--	18 (6 x 3)	20	22
--	72 (12 x 6)	117	314

Results (averaged over 50 trials) for HRM (rigid)/Prob-HRM (articulated) planner

Num. graph vertices	Num. graph edges	Num. path points
841	1883	6
4794	10421	16
1495	2494	24
34197	72063	79
60	140	8
70	174	9
1353	3550	14
1270	2945	12
1854	3994	31
6688	14147	105
367	771	16
36837	83715	20

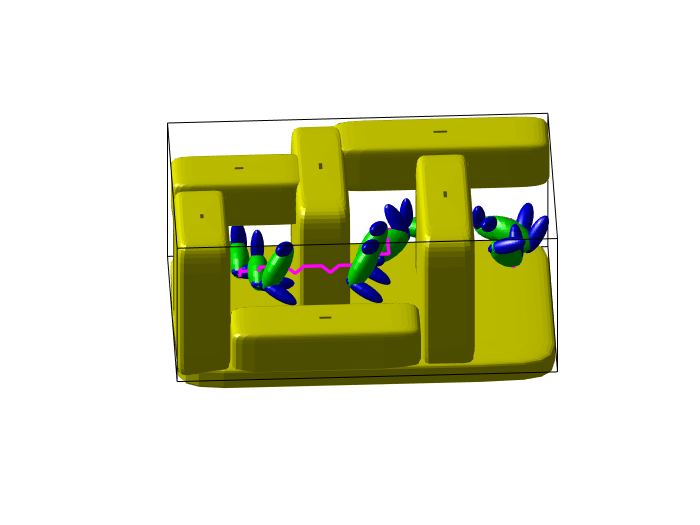
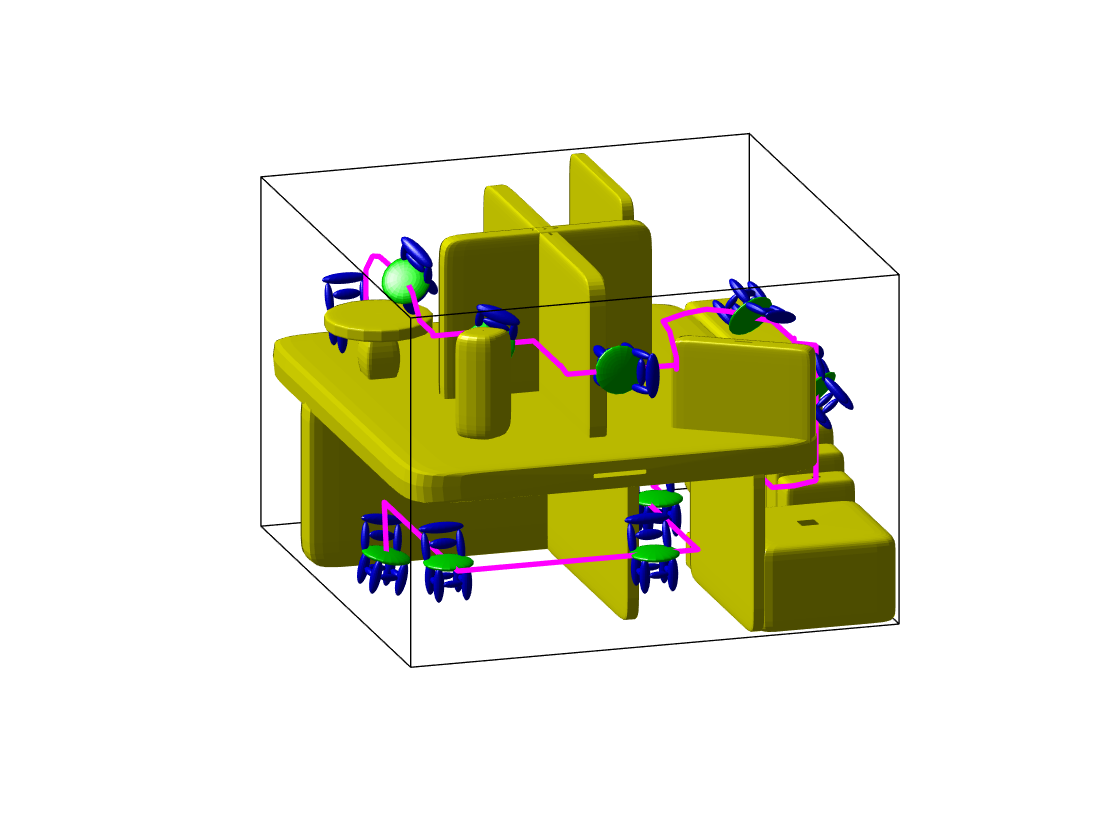
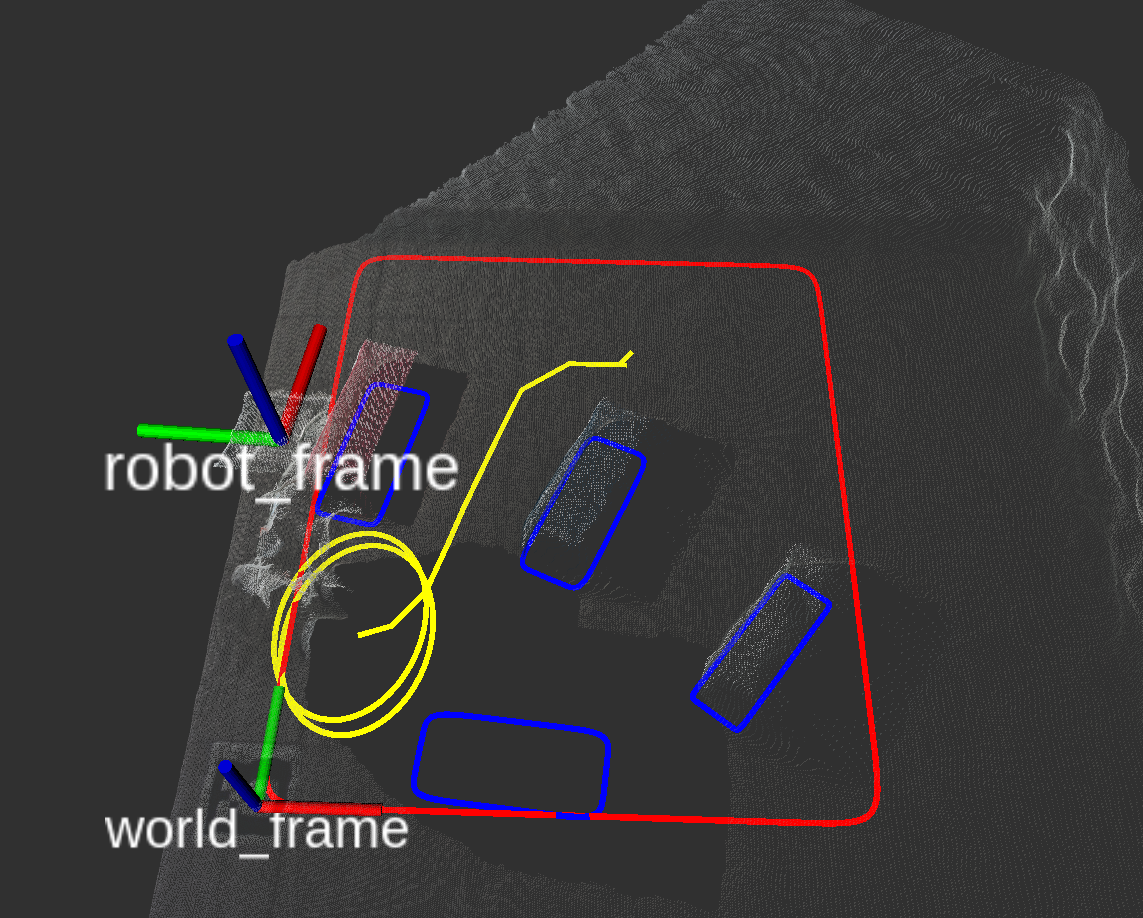
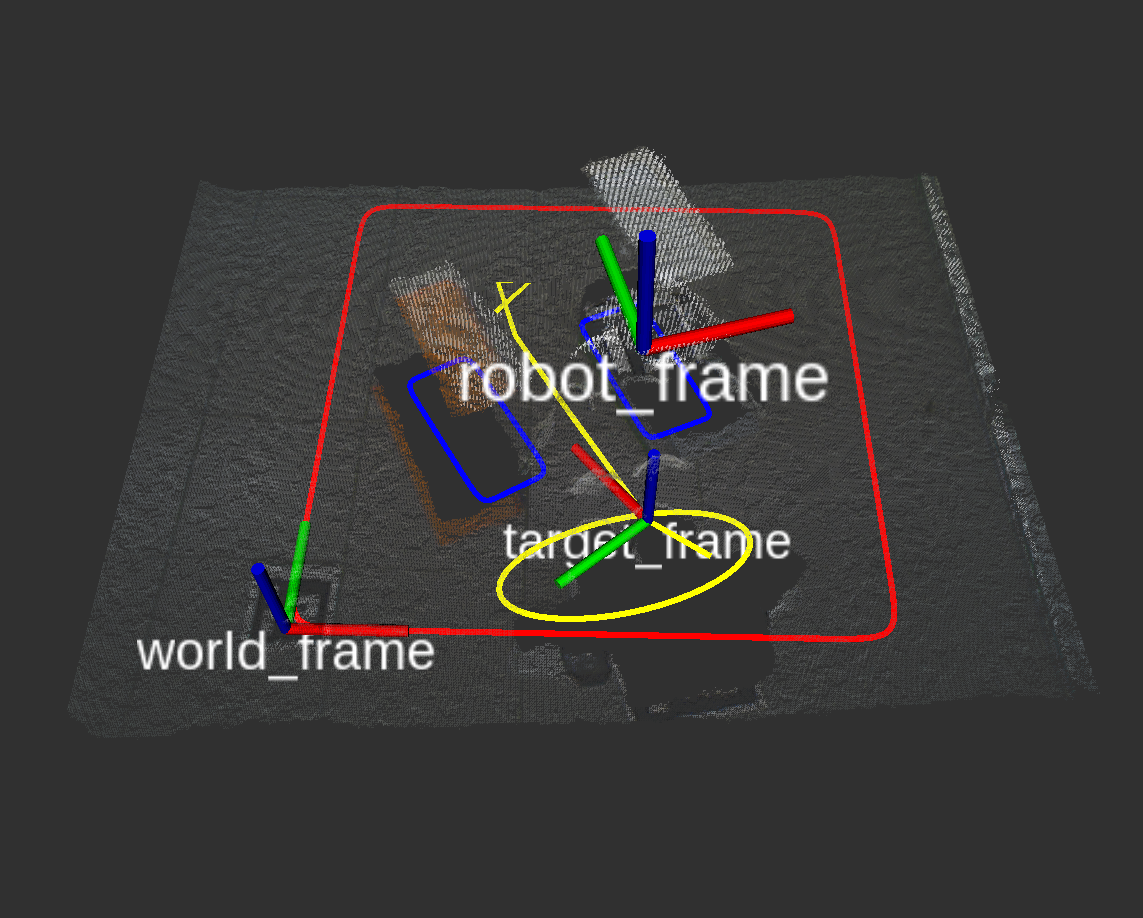
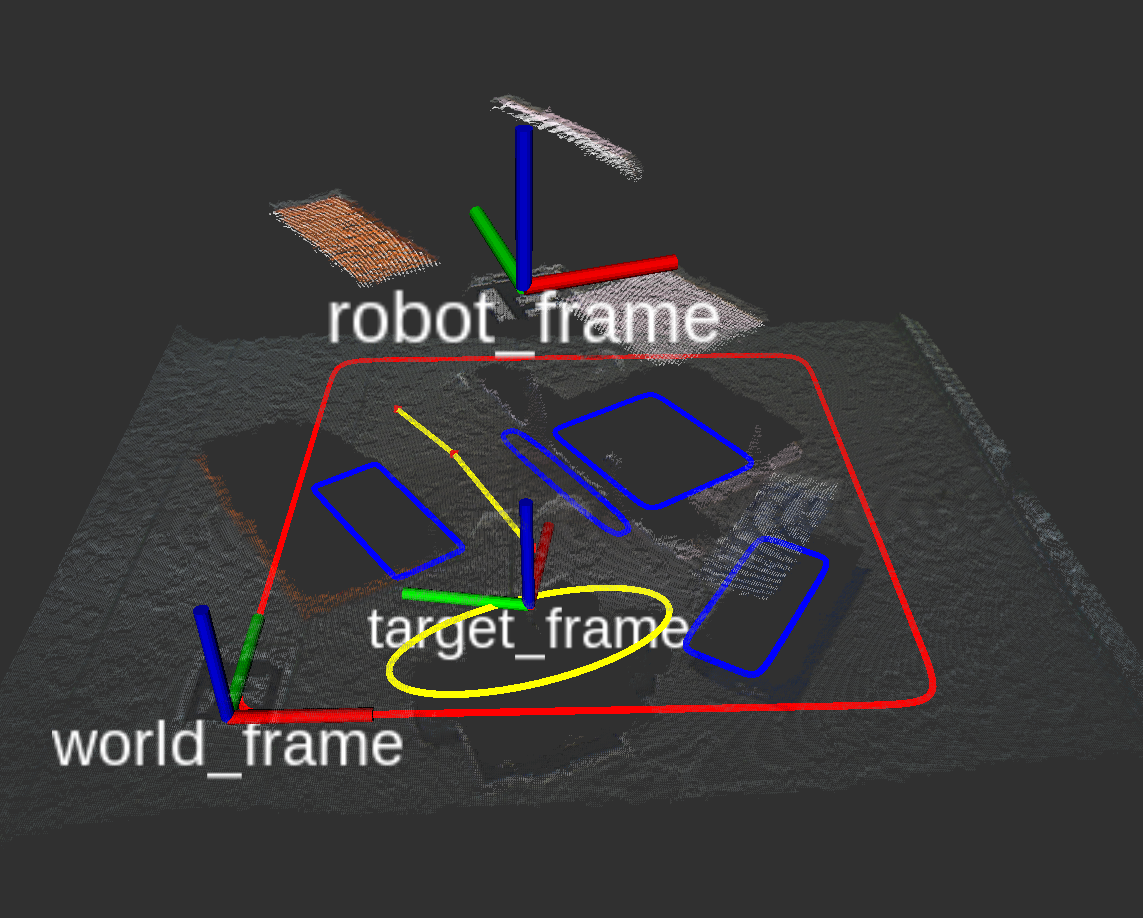
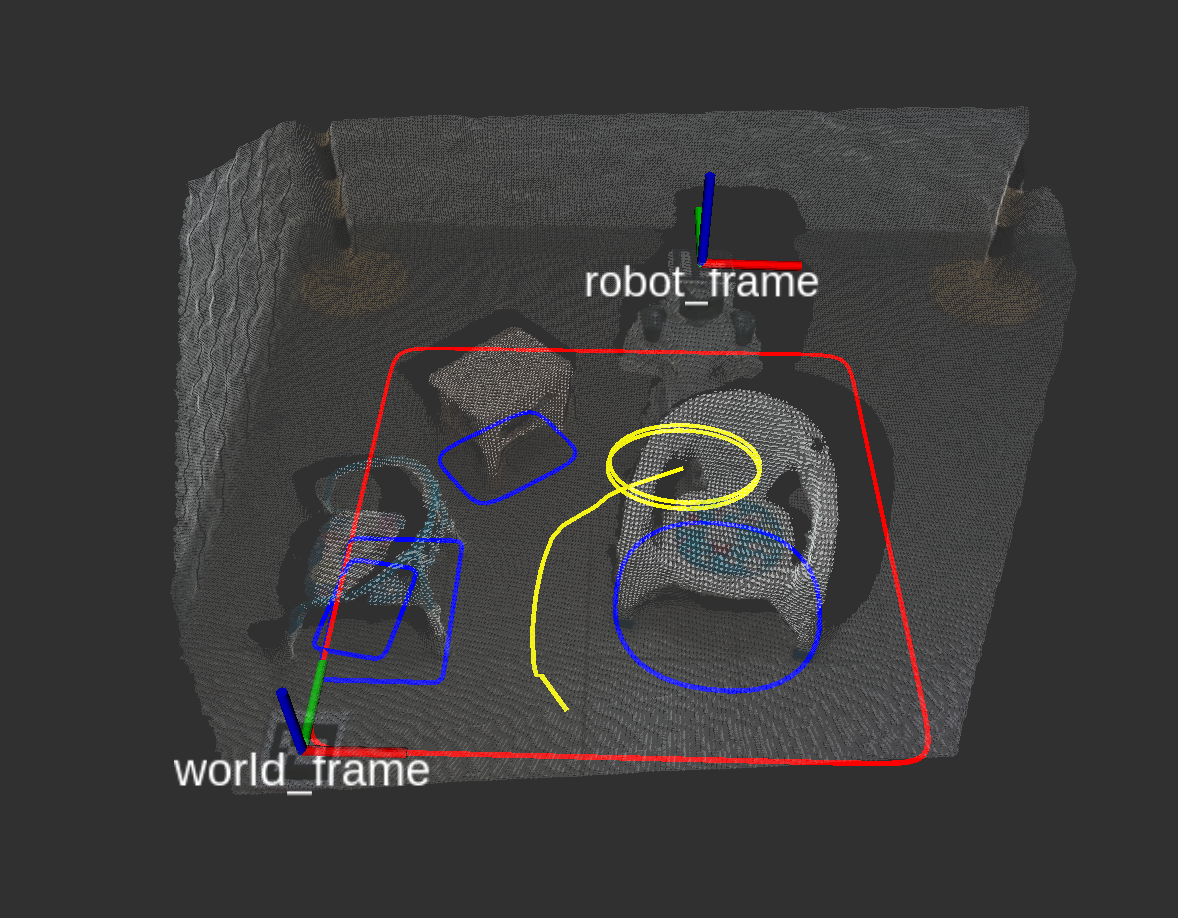
Physical experiments

Choose an example: Experiment 1 Experiment 2 Experiment 3 Experiment 4 Experiment 5

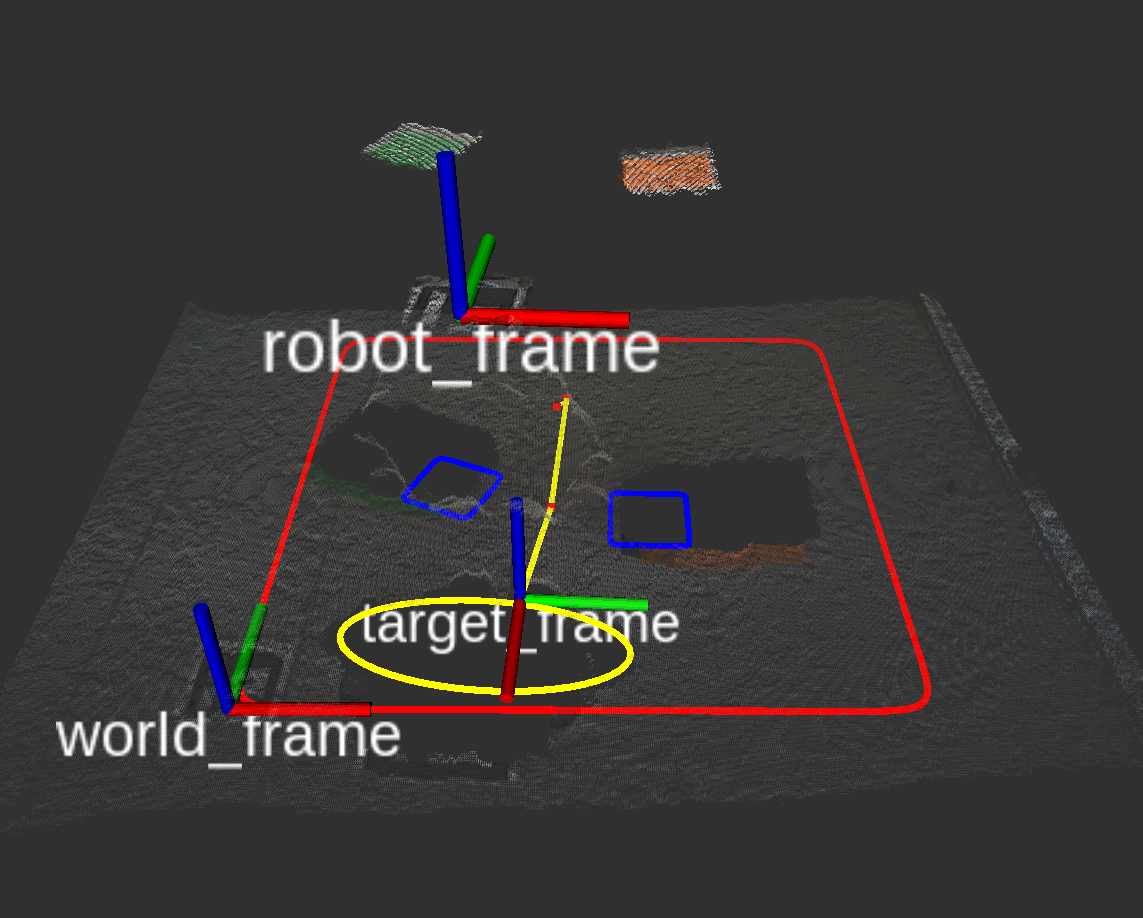
Robot execution screenshot	Planned motion in RViz

Supplementary Video